这篇文章上次修改于 196 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

1.1.二进制思想在计算机科学中的应用

飞书文档链接
1.1.二进制思想在计算机科学中的应用

参考资料

二进制、八进制、十进制、十六进制使用场景_八进制应用在什么地方-CSDN 博客

计算机中不同进制的使用说明_计算机不同进制数怎么使用-CSDN 博客

现代计算机爱上二进制—-为什么要用二进制 - 活着的虫子 - 博客园

二进制是一种基数为 2 的数制，只使用两个数字——0 和 1。这两个数字被称为比特(bit)，是计算机中最小的数据单位。二进制是计算机科学的基础，用于表示所有数据类型。例如，文本通过 ASCII 编码转为二进制，图像和声音也以二进制存储。逻辑电路依赖二进制逻辑门（如 AND、OR、NOT）执行计算，处理器通过二进制指令执行操作。此外，二进制在数字通信、加密技术和错误检测中也至关重要。这些应用确保了现代计算系统的功能。

二进制在计算机科学中的应用

密码学与数据校验

密码学的所有技术实现均基于二进制运算，二进制是计算机处理数据的基础单位，密码学通过二进制操作实现数据的加密、哈希、签名等核心功能。

数据存储与传输所有明文、密文、密钥、哈希值等均以二进制形式存储和传输（如 ASCII 文本需先转为二进制再加密）。
位操作（Bitwise Operations）密码算法依赖二进制位运算（如异或 XOR、移位、置换）实现加密混淆。

示例：AES 加密中的“字节替换（SubBytes）”步骤，本质是二进制字节通过 S 盒（查找表）进行非线性变换。

非对称加密的二进制数学基础

大整数运算
- RSA、ECC 等算法依赖超大二进制整数的运算（如模幂运算、椭圆曲线点运算）。
示例：RSA 加密中，公钥加密过程本质是计算，其中均为二进制大整数。
二进制优化
- 快速幂模运算通过二进制分解指数（如）加速计算。
  假设指数是一个正整数，它可以表示为二进制形式。例如，假设，其二进制表示为。这意味着：
因此，可以将写成：

然后分别计算、以及与求和即可

密钥与随机数的二进制本质

密钥生成
- 对称密钥（如 AES-256 的 256 位密钥）、非对称私钥（如 ECC 的 256 位随机数）均为二进制序列。
- 密钥安全性依赖二进制随机数的不可预测性（如量子随机数生成器）。
密钥存储
- 密钥需以二进制形式安全存储（如硬件加密模块 HSM）。

密码协议中的二进制交互

网络协议
- HTTPS、SSH 等协议中，所有握手、加密、签名过程均通过二进制数据包实现。示例：TLS 协议中，客户端与服务端交换随机数（二进制串）生成会话密钥。
编码与解码
- 加密后的二进制数据需通过 Base64、Hex 等编码转为可传输文本格式。

权限控制

基于二进制的权限管理与验证 - 勤奋的菜鸟 - 博客园

权限控制 | 使用二进制做权限控制功能

使用位运算的权限控制(bitmask)

Linux 权限的二进制表示

Linux 中每个文件/目录的权限分为 所有者（User）、所属组（Group）、其他用户（Others） 三个角色，每个角色对应 读（r）、写（w）、执行（x） 三种权限，分别用 3 位二进制 表示：

rwx r-x r-- → 二进制：111 101 100 → 八进制：754
   ↑   ↑   ↑
  用户 组  其他

• 每个权限位映射：

• r（读）：二进制第 2 位（值 4）

• w（写）：二进制第 1 位（值 2）

• x（执行）：二进制第 0 位（值 1）

• 权限组合：通过二进制位或运算（|）实现，例如：

rw- = 4（r） + 2（w） = 6 → 二进制 110
rwx = 4 + 2 + 1 = 7 → 二进制 111

权限操作的核心逻辑

权限验证

Linux 内核通过 按位与运算（&） 判断用户是否拥有某权限。例如，检查用户是否有执行权限：

// 检查 st_mode 是否包含用户执行权限位
if (st_mode & S_IXUSR) { /* 允许执行 */ }

• 权限位宏定义：

#define S_IRUSR 0400  // 用户读权限（二进制：100 000 000）
#define S_IWUSR 0200  // 用户写权限（二进制：010 000 000）
#define S_IXUSR 0100  // 用户执行权限（二进制：001 000 000）

权限修改

通过 按位或（|）赋予权限 和 按位与非（& ~）移除权限 实现动态调整：

// 添加用户写权限
st_mode |= S_IWUSR;

// 移除用户执行权限
st_mode &= ~S_IXUSR;

用户视角的权限管理

chmod** 命令的底层实现**

• 符号模式：直接操作权限位

chmod u+x file    # 添加用户执行权限（位或运算）
chmod g-w file    # 移除组写权限（位与非运算）

• 八进制模式：直接指定二进制掩码

chmod 755 file    # rwxr-xr-x → 二进制 111 101 101 → 八进制 755

权限继承与默认值

• umask 值：通过二进制掩码定义默认权限的补码

umask 022         # 默认创建文件权限为 644（777 & ~022 = 755）

扩展应用：特殊权限位

Linux 还扩展了 SUID、SGID、Sticky Bit 等权限，仍基于二进制位掩码设计：

• SUID（Set User ID）：二进制第 11 位（八进制 4000）

chmod u+s /usr/bin/passwd  # 设置SUID，允许普通用户以root权限修改密码

• Sticky Bit：二进制第 9 位（八进制 1000）

chmod +t /tmp              # 仅文件所有者可删除自己的文件

权限表示：每个权限对应一个二进制位，组合成八进制数存储。
权限操作：通过位运算（|、&、~）实现动态调整。
高效性：位运算的原子性和低开销保障了权限验证的高效性。
可扩展性：通过扩展位掩码（如 SUID）支持复杂权限需求。

这一设计充分体现了二进制在权限控制中的核心价值——简洁、高效、灵活。

代码示例

#include <bits/stdc++.h>

using namespace std;

const int S_IXUSR = 0400;_ // 用户读权限（二进制：100 000 000）_
const int S_IWUSR = 0200;_ // 用户写权限（二进制：010 000 000）_
const int S_IXUSR = 0100;_ // 用户执行权限（二进制：001 000 000）_

void check_permission(int st_mode)
{
_    // 检查 st_mode 是否包含用户执行权限位_
    if (st_mode & S_IXUSR)
    {
_         /* 允许执行 */_
    }
}

企业级框架的权限控制

算法上的应用

原码反码补码

在计算机中，带符号整数通常用补码表示，其转换流程为：

正数的补码 = 原码；
负数的补码 = （原码取反）+ 1。

值	原码（二进制）	反码	补码
+5	00000101	—	00000101
–5	10000101	11111010	11111011

补码的好处是：加减运算都能统一为加法，省去了符号位处理的特殊逻辑，也天然支持异或、与或等位运算。

位运算

取反（NOT）：~x 将 x 的每一位二进制翻转。
与（AND）：x & y，常用于屏蔽某些位，比如 x & 1 可判断 x 的奇偶。
或（OR）：x \| y，用于将某些位设为 1。
异或（XOR）：x ^ y，相同位结果为 0，不同位结果为 1。
左移（<<）与右移（>>）：将二进制整体左移或右移，等价于乘／除以 2 的幂。

例如，下面函数高效判断一个整数是否是 2 的幂次方：

bool isPowerOfTwo(int x) {
    return x > 0 && (x & (x - 1)) == 0;
}

def is_power_of_two(x: int) -> bool:
    return x > 0 and (x & (x - 1)) == 0

快速幂

快速幂 - OI Wiki

快速幂模运算通过二进制分解指数（如）加速计算。
假设指数是一个正整数，它可以表示为二进制形式。例如，假设，其二进制表示为。这意味着：

因此，可以将写成：

然后分别计算、以及与求和即可

算法思想：

维护结果 res=1；
当最低位时，res *= a；
每次循环后，a *= a（平方），并将右移一位；
重复上述直到，最终 res 即为。

long long fast_pow(long long a, long long e) {
    long long res = 1;
    while (e > 0) {
        if (e & 1)            // 若当前最低位为 1
            res = res * a;
        a = a * a;           // 平方
        e >>= 1;             // 右移下一位
    }
    return res;
}

int main() {
    std::cout << fast_pow(2, 13) << std::endl;  // 输出 8192
    return 0;
}

异或运算

交换变量（无需临时变量）

a ^= b; b ^= a; a ^= b;

找出唯一出现一次的数

对于一个数组中只有一个元素出现一次，其余元素都出现两次，用异或可线性时间、常数空间找出它：

def single_number(nums):
    ans = 0
    for x in nums:
        ans ^= x
    return ans

按位翻转特定范围

将 n 的第 i 到 j 位全部翻转：

int mask = ((1 << (j - i + 1)) - 1) << i;
n ^= mask;

数据的表示、计算、存储和传输

数据压缩

https://colab.research.google.com/drive/1Mmi0GjoN2xCAIsyrTwYswP-FGUwMHEDQ?usp=sharing(colab 链接)

数据压缩可以分为有损压缩（Lossy）和无损压缩（Lossless）两类。

无损压缩在压缩和解压后能够完全恢复原始数据，常见算法有 DEFLATE（gzip、PNG）、LZMA（7z）等。

gzip（无损）示例：

import gzip

text = b"Data compression example. " * 100
# 压缩
compressed = gzip.compress(text)
print("原始大小：", len(text), "压缩后大小：", len(compressed))
# 解压
decompressed = gzip.decompress(compressed)
assert decompressed == text

以上示例使用 DEFLATE 算法，无损地将文本压缩并恢复

有损压缩则在压缩过程中丢弃“人眼/人耳不易察觉”的冗余信息，如 JPEG 图像、MP3 音频，其解压后无法恢复到完全原始状态。

from PIL import Image
img = Image.open("input.png")
img.save("output.jpg", quality=50)  # quality<100 会丢失部分细节

# 对比文件体积
ls -lh input.jpg output.jpg

通过调整 quality 参数，JPEG 有损压缩可在保留较好视觉效果的同时大幅减小文件体积。

OneHot 编码

https://colab.research.google.com/drive/1VpmC-vKrvaFusdNNuaavzvAk2YMhGWrW?usp=sharing(colab 链接)

One-Hot 编码是一种将分类变量转换为稀疏二进制向量的技术，每个类别对应一个维度，只有所属类别位置为 1，其它位置为 0。

Pandas 实现示例：

import pandas as pd
df = pd.DataFrame({"color": ["red", "blue", "green", "blue"]})
one_hot = pd.get_dummies(df["color"], prefix="color")
print(one_hot)

color_blue  color_green  color_red
0       False        False       True
1        True        False      False
2       False         True      False
3        True        False      False

此方法对小规模类别集非常高效，并集成于 Pandas。

Scikit-Learn 实现示例：

from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder(sparse=False)
X = enc.fit_transform(df[["color"]])
print(X)

[[0. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]
 [1. 0. 0.]]

OneHotEncoder 支持 handle_unknown 参数，用于处理训练外出现的新类别。

深度学习中数据与模型的二进制存储方法

深度学习框架通常使用专门的二进制格式保存模型参数和网络结构，以提高读写性能并节省存储空间。

PyTorch：使用 Python 序列化（Pickle）将模型权重保存在 .pt 或 .pth 文件，通常调用 torch.save(model.state_dict(), 'model.pth') 和 model.load_state_dict(torch.load('model.pth'))。
TensorFlow：采用 SavedModel 格式，目录中包含 saved_model.pb（Protobuf 二进制）与 variables 检查点文件，使用 model.save('path') 和 tf.keras.models.load_model('path') 进行读写。
安全张量（safetensors）：新兴格式，提供比 Pickle 更强的安全性与加载性能，示例：

import safetensors.torch as st
st.save_file(model.state_dict(), "model.safetensors")

此外，ONNX（Open Neural Network Exchange）以 Protobuf 二进制保存跨框架模型结构与权重，易于在不同平台间互操作。

CSS 等设计方面的颜色编码

在前端设计中，颜色可通过多种编码表示，最常见的是十六进制（Hex）、RGB(A) 与 HSL(A) 格式。

Hex：#RRGGBB 或简写 #RGB，例如 #ff00aa。
RGB：rgb(255,0,170)，可加透明度：rgba(255,0,170,0.5)。
HSL：hsl(320,100%,50%)，直观调节色相、饱和度、亮度。

CSS 示例：

.button {
  background: #3498db;           /* Hex */
  color: rgb(255, 255, 255);     /* RGB */
  border-color: hsl(200, 70%, 50%); /* HSL */
}

JavaScript 转换示例：

// Hex to RGB
function hexToRgb(hex) {
  let m = hex.match(/^#?([A-F\d]{2})([A-F\d]{2})([A-F\d]{2})$/i);
  if (!m) return null;
  return {
    r: parseInt(m[1], 16),
    g: parseInt(m[2], 16),
    b: parseInt(m[3], 16)
  };
}
console.log(hexToRgb("#ff00aa")); // {r:255, g:0, b:170}

计算机网络 ip 地址

计算机网络（一）基本概念（IP,子网掩码,默认网关,DNS）
【计算机网络】IP 协议、IP 地址、网段划分、子网划分、子网掩码、CIDR_ip cidr-CSDN 博客
 IP 地址、子网掩码、网关、DNS 之间的关系

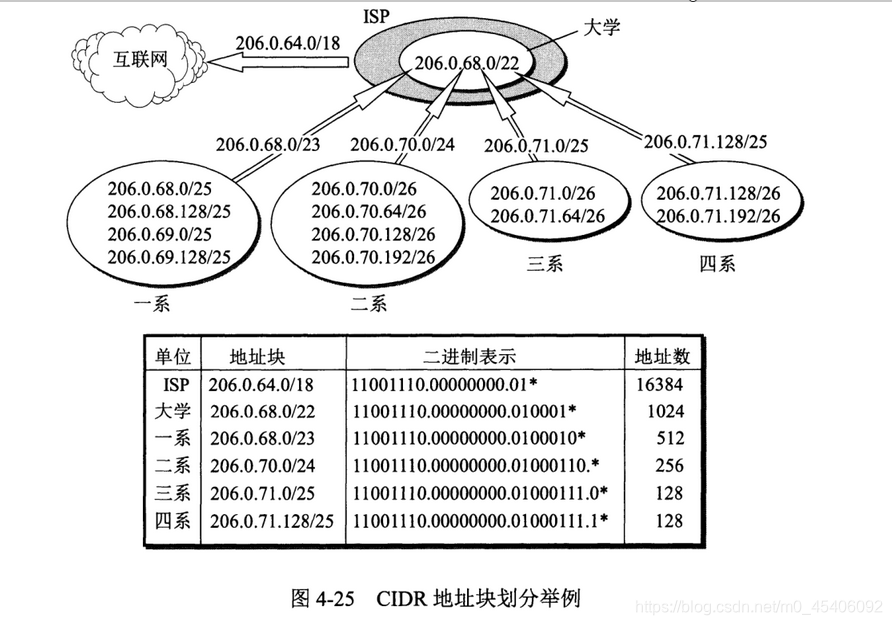
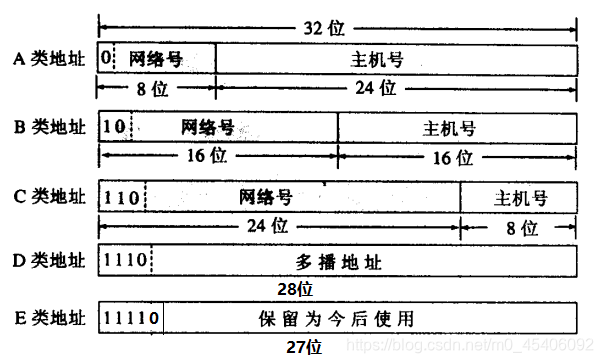
IP 地址、子网掩码、默认网关与 DNS 协同完成局域网与互联网互联：

IP 地址：标识主机在子网中的唯一地址，如 192.168.1.10/24。
子网掩码：如 255.255.255.0（/24），用于划分网络号与主机号。
默认网关：同子网内路由器接口地址，负责跨网段转发，如 192.168.1.1。
DNS：域名解析服务器，将域名映射至 IP（如 8.8.8.8）。

ipaddress 计算示例：

https://colab.research.google.com/drive/1rXH5_RbucvYiemz9kz4mfqlx1Uz3DWA2?usp=sharing(colab 链接)

import ipaddress

net = ipaddress.ip_network("192.168.1.10/24", strict=False)
print("网络地址:", net.network_address)
print("广播地址:", net.broadcast_address)
print("可用主机:", list(net.hosts())[:3], "…共", net.num_addresses - 2)

TK的小站

2025-04-15-二进制思想在计算机科学中的应用